Mathematical Morphology: Basics
Mathematical morphology is a way of treating images without altering the shape of the objects in the images. It is is based on set theory. The shapes of objects in a binary image are represented by object membership sets. This theory can be extended to gray scale images. Morphological operations can simplify image data, preserving the objects’ essential shape characteristics, and can eliminate irrelevant objects.
Mathematical morphology is based on two basic operations: dilation, which fills holes and smoothens the contour lines, and erosion, which removes small objects and disconnects objects connected by a small bridge. Note: dilation and erosion are each other's complement, so actually there only one basic operator. Such operations are defined in terms of a structuring element, a small window that scans the image and alters the pixels in function of its window content. The choice of the proper structuring element is important. Opening and closing are combinations of a dilation and an erosion.
Some examples of structuring elements (the X is the origin of the element; taking another origin will give different results):
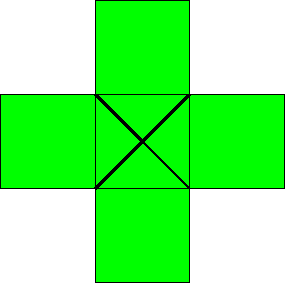 cross
shaped
cross
shaped 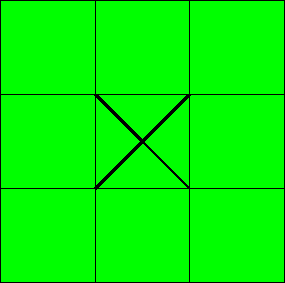 square
shaped
square
shaped  disk
shaped
disk
shaped
The main advantage of a morphological filter is the ability to preserve the shape of large enough objects, unlike a Gaussian filter which blurs the image. Morphology can also be used to segment regions of interest from an image. It also provides a basis for the theory of the pattern spectrum which gives a histogram of the distribution of the sizes of various objects comprising an image. The parameters distilled from this spectrum allow us to perform a quantitative analysis of the content in the image.
